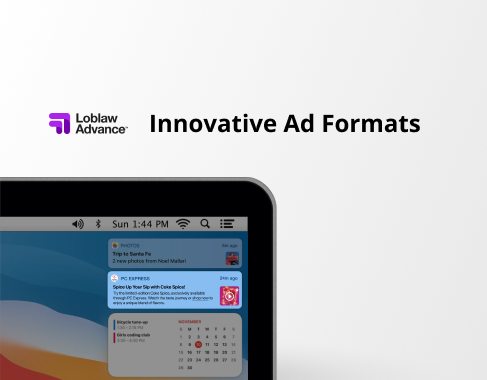
Ad Innovation (case study)
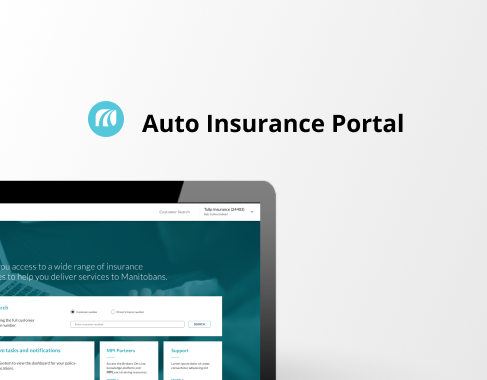
Auto Insurance Platform (case study)

Visual Design

Energy Service Portal (case study)

Internal AI Bot Design

Empowered 4X (case study)
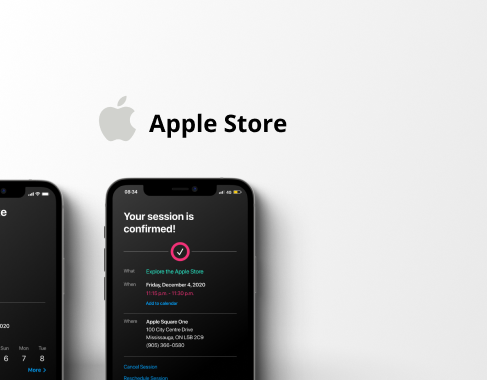
Apple Store Support [upgraded] case study

Washingo (case study)
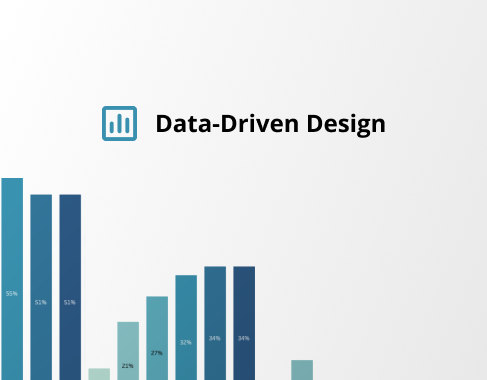
Usability & Data Driven Design